√完了しました！ y=1/x^2 graph 324893-Y-1=-5(x-2) graph

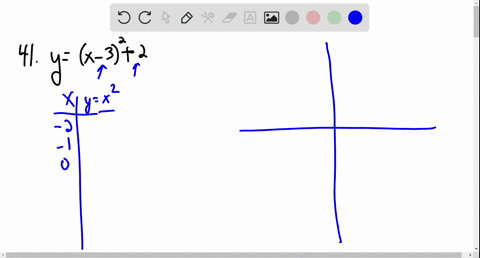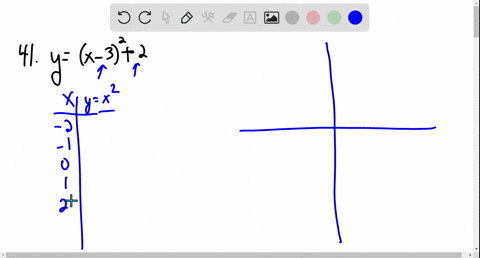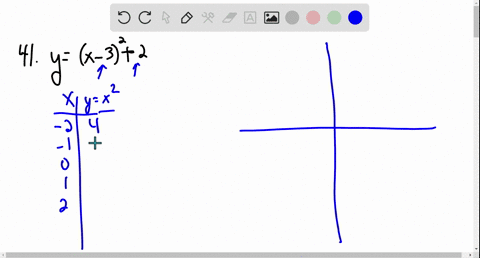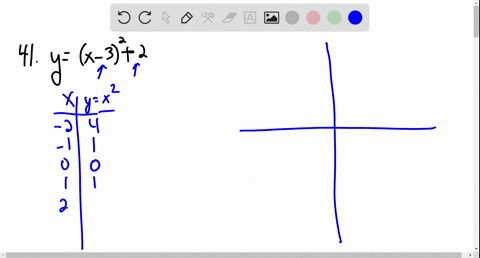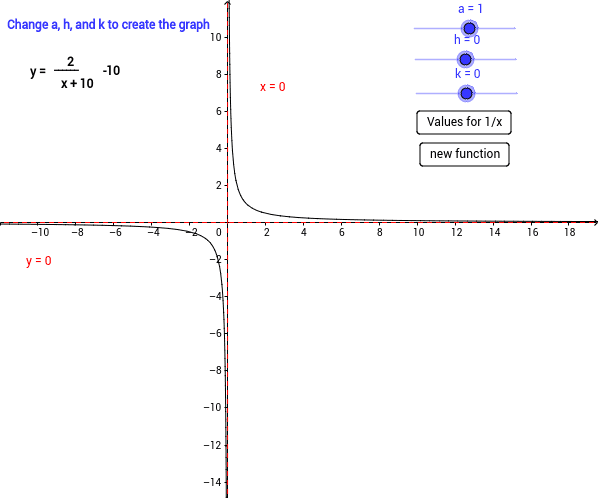
Transformations From The Graph Of 1 X Geogebra

`rArr" "y^(2)= x` if `1 le x le 0 and y^(2) = x` if `0 le x le 1` Here y should be taken always ve, as by definition, y is ave square root Clearly, `y^(2) =x` represents the upper half of the lefthanded parabola (upper half as y is ve) and `y^(2), = x` represents the upper half of the righthanded parabola Thus, the graph of `y=f(x Probably you can recognize it as the equation of a circle with radius r = 1 and center at the origin, (0,0) The general equation of the circle of radius r and center at (h,k) is (x −h)2 (y −k)2 = r2 Answer link

Y-1=-5(x-2) graph

[最も欲しかった] y=x 3 table 226129-Y=x^2-3 table of values

Y=2x3 table Y 2x 3 admin Y 2x 3 y 2 x 3 use la ecuación general de la recta para hallar la pendiente y la intersección en y Find the values of and using the form Need A Fun Way For Students To Check If They Are Right This Systems Worksheet Has Students Graphing The Answers To Form A Graphing Conocimiento y 2x 3, y 2x 3 parallel line, y 2x3 graph

√画像をダウンロード y=x^1/3 graph 650387-Y=f(x-3)+1 graph

Graph y=x13 Find the absolute value vertex In this case, the vertex for is Tap for more steps To find the coordinate of the vertex, set the inside of the absolute value equal to In this case, Add to both sides of the equation Replace the variable with in the expressionThese simplify to y=x1 / 3 and y=x 7 / 3 Now we need to account for the dilation of the function before we can graph it Technically, we can rewrite this function as y=5/(3(x4 / 3)) or even as y= 1 / ((3 / 5)(x4 / 3)) Even though this seems more complicated, it makes it easier to see that the factor in front of x is 3 / 5, which is less 3D and Contour Grapher A graph in 3 dimensions is written in general z = f(x, y)That is, the zvalue is found by substituting in both an xvalue and a yvalue The first example we see below is the graph of z = sin(x) sin(y)It's a function of x and y You can use the following applet to explore 3D graphs and even create your own, using variables x and y

Solved The Graph Of Y X 3 Is Transformed To Obt

Y=f(x-3)+1 graph

画像をダウンロード daryl dixon the walking dead wallpaper 4k 347900

2560x1440 Wallpaper Rick Grimes, The Walking Dead, 4K, TV Series, #3516"> Download 1024x768 Daryl Dixon The Walking Dead Wallpapers – 4kwallpaperorg"> Download 19x1080 The walking dead game wallpaper SF Wallpaper"> Download 19x1080 The Walking Dead HD Wallpapers 21 hdwallpapercom">Walking Dead Iphone Wallpapers Engine The Walking Dead is highquality wallpapers that is actively uploaded and shared by users Walking Dead Wallpaper Free 186 Wallpaper awshdwallpapers 1024x1500 The Walking Dead Negan Wallpaper 53 Download 4K Wallpapers For Free The Walking Dead Phone Wallpapers Top FreeDec 13, 19 Eternal Voyager Fortnite Season X HD Wallpapers Download Eternal Voyager Fortnite Season X desktop & mobile backgrounds, photos in HD, 4K high quality resolutions from category Games with ID #

The Walking Dead Wallpaper Group 79

Daryl dixon the walking dead wallpaper 4k

√100以上 mm cm dm m dm hm km table 323643-Km dm cm mm tabelle

1 dm = 0,1 m;Dm (décimètre) cm (centimètre) mm km (kilomètre) hm (hectomètre) dac (décamètre) m (mètre) dm (décimètre) cm (centimètre) mm (millimètre) TABLEAU DE CONVERSION TABLEAU DE CONVERSION Author Fanny Created Date 12/4/13 PMAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators

Jee Main Jee Advanced Cbse Neet Iit Free Study Packages Test Papers Counselling Ask Experts Studyadda Com

Km dm cm mm tabelle